The Basics of Killer Sudoku

In this post I’ll walk you through how to solve this puzzle, Glider, which I designed to highlight several of the most fundamental elements of killer sudoku logic. Click any of the links below to try it yourself!

• Fill each row, column, and 3x3 box with the digits 1-9 once each.

• The sum of the digits inside each cage is equal to the small number in the top left corner. Digits cannot repeat within a cage.

• Very rough difficulty estimate: 4/10

Play online: SudokuPad | unshaded | F-Puzzles | unshaded

---

I want to note at the top that my goal here is to show a variety of types of logical deductions that can be useful in killer sudoku. Some of them may be more intuitive to you than others, and that’s fine—most, if not all, of the deductions described below can be reached in multiple equally valid ways.

Ok, on to the walkthrough. Item #2 below is surely the most important thing to know, but in the spirit of starting at the start, when I solve a puzzle the first thing I look for is…

1. Extreme cage sums

For any given cage size (between two and seven cells), there are four sums—two at the low end and two at the high end—that can only be filled with one combination of digits. Here are all of those combinations for two-, three-, and four-cell cages:

2. The Rule of 45

Or the Law of 45, or The Secret, or whatever you want to call it. Point is:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45

…and this is very powerful in killer sudoku. In the example above, the sum of the digits in the blue cells (6 + 24 + 9) is 39, and the sum of all of the digits in box seven (1-9 once each) is 45, so the only unshaded cell in the box must be equal to 45 - 39, which is 6.

This also works for a collection of cells extending from a box (or row or column). Here, the sum of the digits in the red cells (10 + 6 + 18 + 15) is 49, and the sum of all of the digits in box nine is 45, so the cell in this cluster that falls outside of box nine must be equal to 49 - 45, i.e. 4.

The tricks shown in the next screenshot are probably closer to intermediate than beginner-level, but they’re examples of some of the less straightforward ways the Rule of 45 can be used (this is just the tip of the iceberg in that regard).

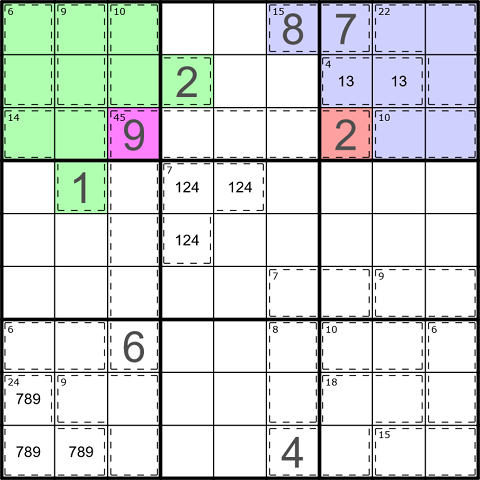
I’ll start with the top-right corner. The sum of the digits in the blue cells (15 + 22 + 4 + 10) is 51, which is 6 greater than the sum of the digits in box three. Since the only differences between those two collections of cells are r1c6 (part of the blue cells but not box three) and the red cell (part of box three but not the blue cells), the digit in r1c6 must be 6 greater than the digit in the red cell. This means the red cell must contain 1, 2, or 3, and the 4-cage in the box means it must be a 2.

The top-left shaded cells are in a more complex, but similar, pattern. The sum of the digits in the green cells (6 + 9 + 10 + 14) is 39, which is 6 less than the sum of the digits in box one. This means the digit in the purple cell must be 6 greater than the sum of the digits in r2c4 and r4c2. In theory it could be an 8 with two 1s, but the 4-cage in row two makes that impossible.

3. Remember, digits cannot repeat within a cage

It’s easy to neglect this aspect of killer sudoku (and in some puzzles the rule is largely irrelevant), but any time a puzzle features cages that span multiple boxes it’s wise to think about the implications. Here, the 2s in r2c4 and r3c7 rule 2 out of every other cell in those cages, which means the 2 in column three must be in either r8c3 or r9c3, and either way the 6-cage in box seven must contain 1 and 5.

4. Consider how cages interact with each other

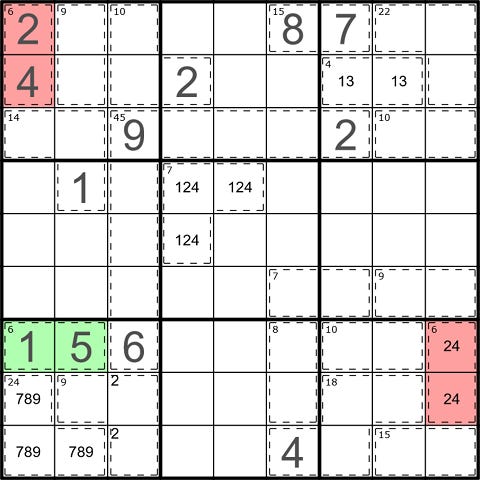
A two-cell cage that sums to six must be filled in one of two ways: 1-5 or 2-4. Once the cage in box seven is known to be 1-5, it actually resolves the other two 6-cages in the puzzle. In box one, both cells see the 1 in r7c1, so the cage can never be filled with 1-5. Meanwhile, r7c9 sees both cells of the box seven cage, so the box nine cage can also never be filled with 1-5.

Along somewhat similar lines, here’s a deduction that can be made in rows eight and nine:

The 15-cage can be filled in one of two ways: 6-9 or 7-8. But two cells in the 24-cage share a row with the 15-cage—if it contained 7-8, it would be impossible to complete the row without repeating a 7, 8, or 9 somewhere.

5. Use what you know about a cage’s properties to narrow down options

This one’s pretty vague—apologies!—but the idea I’m getting at is that you don’t have to be a supercomputer to solve killer sudokus. Once you have a few digits placed, there are plenty of logical shortcuts available to help resolve even the most average-seeming cages.

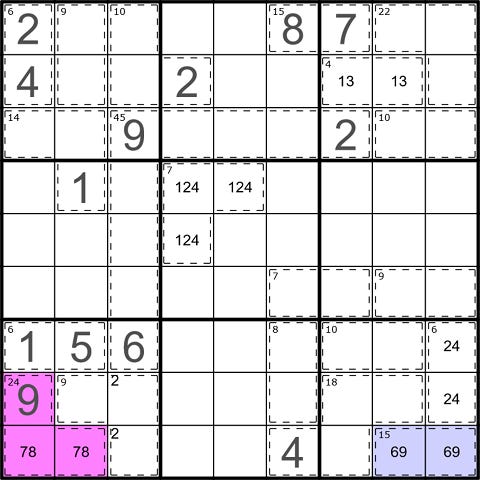
For example, a two-cell 9-cage must contain exactly one low digit (1-4) and exactly one relatively high digit (5-8). The 9-cage in box one sees a 2 and 4 in its box and a 1 in its column, so its low digit must be 3, which must be accompanied by 6. Similarly, a two-cell 10-cage needs one low digit (1-4) and one high digit (6-9), and the only available low digit in box three is 4.

A few more things that are always true about two-cell cages (assuming standard rules, of course), where N represents the sum:

• If N is odd, the cage must contain one odd digit and one even digit.

• If N is even, the cage must contain two digits with the same parity.

• If N is less than 10, the highest digit that can appear in the cage is N-1.

• If N is greater than 10, the lowest digit that can appear in the cage is N-9.

• The cage can never contain N/2 (e.g. a two-cell 8-cage can never contain a 4).

Ok, I’ll leave it there. If you’ve been following along, you should be able to solve the puzzle from here using nothing more fancy than regular sudoku and simple arithmetic (keep scrolling to see the solution).

I hope you’ve found this helpful! If you have any questions or feedback, please feel free to leave a comment or reply to an Artisanal Sudoku email.