Artisanal Sudoku, Volume 90

1. Centerpiece

• Fill each row, column, and 3x3 box with the digits 1-9 once each.

• The sum of the digits inside each cage is equal to the small number in the top left corner (if given). Digits cannot repeat within a cage.

• Very rough difficulty estimate: 3/10

Play online: SudokuPad | unshaded | F-Puzzles

New to variant sudoku? Check out these beginner-friendly guides to killer cages and other popular rulesets.

---

Many of you are aware, I’m sure, that 1+2+3+4+5+6+7+8+9 = 45, and in recognition of that fact I made Volume 45 of Artisanal Sudoku a special, non-paywalled preview of the regular weekly bonus content. Well, we’ve made it through 45 more, so it’s time to do it again.

Below, past the point where the post usually comes to an abrupt end for free subscribers, you’ll find two more bonus puzzles, and you’ll find hints for all five of this week’s puzzles below that. For just $5/month, you can get those extras every week, along with full access to the archive (which now contains over 400 puzzles!) and the ability to post and view comments. And even if you don’t want extra puzzles, or don’t need hints, your support is what makes it possible for me to continue putting time and effort and resources into making this the best product it can be.

But this isn’t just about asking for money, it’s about expressing appreciation for free and premium subscribers alike. Few things bring me more joy than this newsletter, and that surely would not be the case if I was just sending it off into the void. So thanks for subscribing, reading, and solving. Thanks for reaching out with nice comments or thoughtful feedback or to ask for help. Thanks for helping to spread the word. Thanks for everything.

Here’s to 45 more, and then some.

---

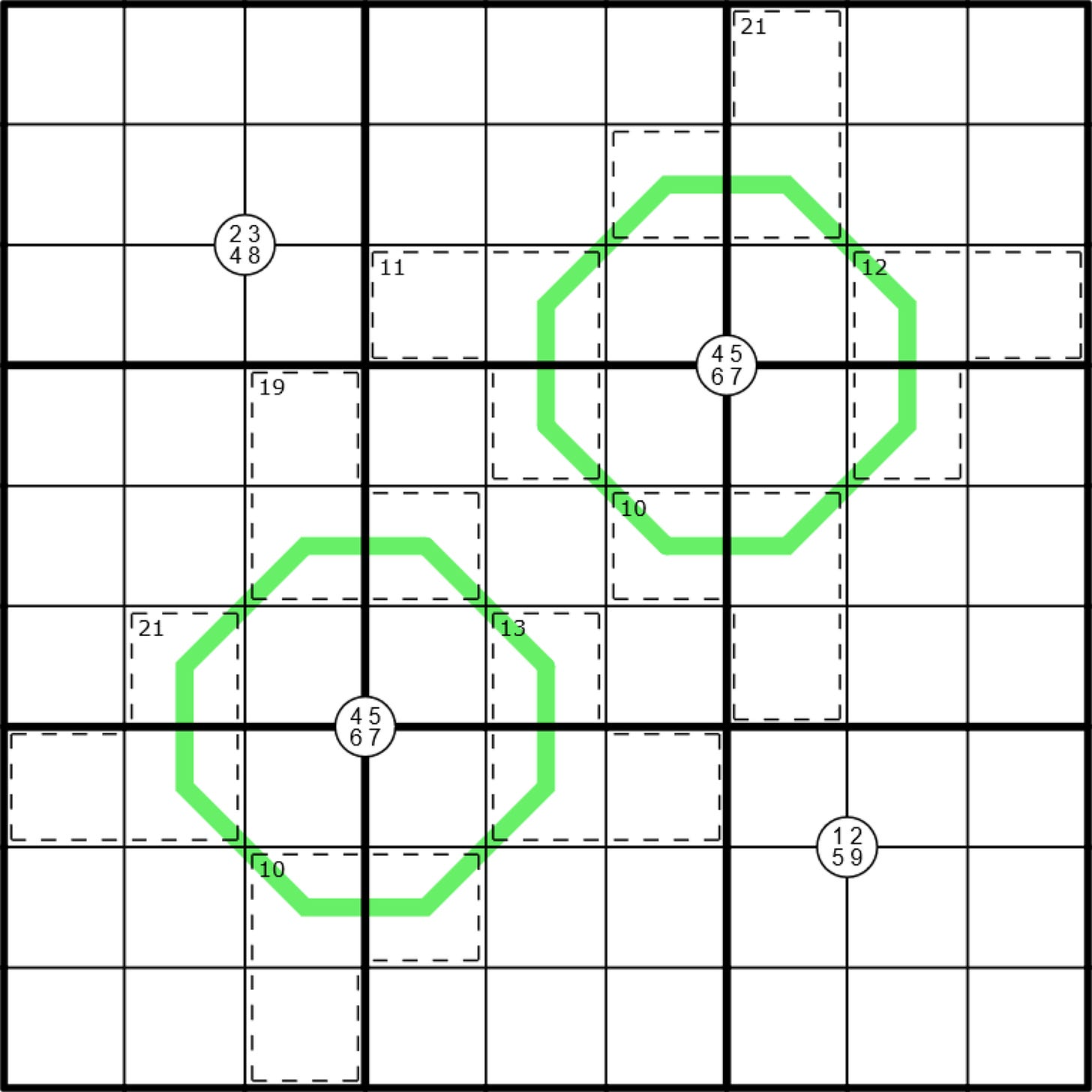
2. Bubble Wrap

• Fill each row, column, and 3x3 box with the digits 1-9 once each.

• The sum of the digits inside each cage is equal to the small number in the top left corner. Digits cannot repeat within a cage.

• Along green lines, digits must differ from their neighbors by at least 5.

• A digit inside a white circle must appear in at least one of the four cells surrounding that circle.

• Very rough difficulty estimate: 5/10

Play online: SudokuPad | F-Puzzles

---

3. Repetition

• Fill each row, column, and 3x3 box with the digits 1-9 once each.

• The sum of the digits inside each cage is equal to the small number in the top left corner. Digits cannot repeat within a cage.

• The sum of the digits along an arrow is equal to the digit in the connected circle. These digits can repeat if allowed by other rules.

• Digits in cells with a shaded square must be even.

• Very rough difficulty estimates: 7/10, 5/10

Play online: SudokuPad | unshaded | F-Puzzles

Extra clues: SudokuPad | unshaded | F-Puzzles

---

4. Smokestack

• Fill each row, column, and 3x3 box with the digits 1-9 once each.

• Correctly placed digits clear the fog around them.

• The sum of the digits inside each cage is equal to the small number in the top left corner. Digits cannot repeat within a cage.

• Digits in cells with a shaded circle must be odd.

• Orthogonally adjacent cells cannot contain consecutive digits (e.g. 6 can never be next to 5 or 7).

• Very rough difficulty estimate: 5/10

Play online: SudokuPad

---

5. El Paso

• Fill each row, column, and 3x3 box with the digits 1-9 once each.

• Digits in columns 1, 5, and 9 indicate the column in which the digit 1, 5, or 9 (respectively) appears in that row (e.g. if there is a 7 in r3c1, then there must be a 1 in r3c7).

• The sum of the digits along an arrow is equal to the digit in the connected circle. These digits can repeat if allowed by other rules.

• Very rough difficulty estimate: 8/10

Play online: SudokuPad | F-Puzzles

---

Thanks for subscribing to Artisanal Sudoku! Feedback is always appreciated, just leave a comment, reach out on Twitter X, or reply to this email. If you liked these puzzles, you probably know someone else who’d like them too, so please spread the word.

---

Hints

Centerpiece

1. Several of the cages can be pencilmarked right off the bat:
   - a two-cell 4-cage must contain 1+3
   - a two-cell 16-cage must contain 7+9
   - a two-cell 17-cage must contain 8+9
   - a three-cell 6-cage must contain 1+2+3
   - a three-cell 7-cage must contain 1+2+4
   - a three-cell 23-cage must contain 6+8+9

2. Consider where 1 and 2 can go in the nine-cell cage. They’re ruled out of r3c6 and r3c7 by the 7-cage, and ruled out of all of the box five cells by the 6-cage, leaving only r6c3 and r7c3.

3. The digits in r3c6 and r3c7 must appear somewhere in box five but cannot repeat in the nine-cell cage. They can’t be 1 or 2 for the reason noted above, which means one of them must be 3 and the other is the same as the digit in r4c4 (which can be determined by considering which digit appears in both the 16-cage and the 23-cage).

Bubble Wrap

1. The cages most restricted by the German whispers are the 21-cages. The only way a three-cell 21-cage can have two digits with a difference of five or more is for those two digits to be 4 and 9, with 8 in the remaining cell.

2. Since each whisper is a loop, any cell that contains a 4 must be flanked by two 9s. This means the 4 in the upper 21-cage must be in r2c7; otherwise, there would be a 9 in a three-cell 11-cage. Similar logic applies to the other whisper.

3. Once you’ve worked out the low/high polarity of the whispers, it should be possible to reduce the options for r4c5 to 6 or 7. But consider what would happen if it contained a 6: it would have to be between two 1s on the whisper, which would put a 4 in r3c4 to fill out the 11-cage, but that (along with the 4 in r2c7) would make it impossible to put a 4 on the quadruple circle in box one.

Repetition

1. Consider where 8 and 9 can go in box one: by sudoku they’re ruled out of the 16-cage, and they can’t be on an arrow because that would imply the digit in the connected circle is 10 or greater, so they must be in r2c2 and r3c3.

2. The maximum sum of three different digits without 8, 9, or 7 is 15 (4+5+6), so the 16-cage must contain a 7, accompanied by two digits that sum to 9, which can be 3+6 or 4+5.

3. A three-cell arrow cannot have a sum less than 3, so the 1 and 2 in box one must be in r2c3 and r3c2. Now, the Rule of 45 can be used to determine that the digits in r1c3 and r3c1 sum to 9 (which makes sense—with the 7 in the 16-cage along with either 3+6 or 4+5, the other of those two pairs will be left on the circles).

4. Since the digits in r1c3 and r3c1 sum to 9, the digits on the connected arrows must also sum to 9. It is impossible, however, for any one digit to appear in more than three of those six cells,* so the only way the combined sum can be as low as 9 is for the arrows to contain three 1s and three 2s.
   *There are probably a few ways to see this. One is to note that if the same digit is in both r3c4 and r4c3, it would be ruled out by sudoku from appearing anywhere else on the arrows, and any other arrangement where a digit appears on the arrows four or more times would require it to repeat in box one or box five.

5. At this point it may be helpful to use shading to distinguish the 12-pairs. For example, the digits in r2c3 and r3c2 must be different (obviously), so the digit in r3c4 must be the same as the digit in r2c3, and so on.
   One conclusion that can be drawn from this is that one arrow contains three 1s and the other contains three 2s, which means the digits in the circles are 3 and 6.

6. Consider what can go in the circle in r8c3. There is a 12-pair in the column, so the minimum sum is 7 (3+4), which is also the maximum due to the 17-cage in box seven.

7. The 12-pair in box five means the digits in r5c6 and r6c5 must sum to at least 7.

Smokestack

1. The 11-cage extends into r8c6, so it must contain at least four cells, which in fact is its maximum size, and the digits in the cage must be 1+2+3+5.

2. The non-consecutive rule means 2 can never be next to 1 or 3, which makes it very difficult to place in the 11-cage. It can’t be in r6c6 or r7c6 because at least one of the adjacent digits in the cage would have to be 1 or 3, and it can’t be in r6c7 because of the odd circle, so the 2 must be in r8c6 (and the 5 must be in r7c6).

3. With 2 and 5 placed in box eight, the options for the two-cell 7-cage are 1+6 or 3+4. But the cage can’t contain 3 and 4 because that would break the non-consecutive rule.
   (Similar logic can be used with any two-cell cage with an odd sum, of which there are several in the puzzle. For example, a two-cell 11-cage cannot contain 5+6.)

4. The 6-cage in box nine can’t be a three-cell cage for several reasons, the simplest being that there can never be a three-cell 6-cage in a puzzle with a non-consecutive rule (wherever the 2 is, there would have to be a 1 or 3 next to it).

5. If there is a 9 in r3c6, it becomes impossible to place 9 in box six. (I realize this means nothing if you’re reading ahead. It’s always awkward to write hints for the later stages of fog puzzles.)

El Paso

1. There’s a very important thing to know about 159-indexing puzzles: any set of three index cells in the same box (say, r1c1, r2c1, and r3c1) must contain one low digit (1-3), one middle digit (4-6), and one high digit (7-9). Any other arrangement would cause the digit being indexed to repeat in a box.
   For example, imagine there is a 4 in r2c1 and a 5 in r3c1. That would imply that there are 1s in r2c4 and r3c5, both of which are in box two.

2. The digit in the circle in r4c1 must be greater than 6, because there must be a middle and high digit in the index cells in box four (for the reason described in hint #1). But it cannot be 9, because that would put a 1 in the circle in r4c9, so the only options are 7 or 8.
   The digit in r4c5 must also be 7 or 8. It can’t be 6 for the same reason noted above, and it can’t be 9 because a 5 in r4c9 would make it impossible to put a high digit in an index cell in box six.

3. The high digit on the index cells in box six must be in the circle, because it must be higher than the digits on the arrow, and the 78-pair in row four leaves 9 as the only option. The digits on the arrow, then, must be 3+6, because that is the only combination that includes a low digit and a middle digit.

4. The three-cell arrows in columns one and five must each have a 1 (since their sums are 7 and 8 and neither can have a repeated digit). But the 1 on the column five arrow cannot be in r7c5, because that would put a 5 in r7c1, making the column one arrow impossible to fill without violating the logic described in hint #1.
   So, one of r5c5 or r6c5 is 1, which means the 5 in column one is in r5c1 or r6c1—either way, there is a 5 on the column 1 arrow, so that must be the arrow that sums to 8.

5. Consider whether the digit in r1c9 can be high. It can’t be 9 because there is already a 9 in r4c9, and it can’t be 7 or 8 because that would put a 9 on the arrow. But it must be at least 4 for the arrow sum to work, so the only options left are 4 and 5 (with 6 ruled out by sudoku).

6. The digits in r1c7 and r1c8, now, must be low, and there still must be a low digit in the index cells in box three, so that digit can’t be in r3c9 because that would force yet another low digit (the fourth in the box) into r3c8. So the low indexing digit is in r2c9, which means the digit in r3c9 must be high, but it can’t be 8 because that would put a 9 on the arrow in r3c8.

7. The 8 and 7 in r4c1 and r4c5 (respectively) put 1 in r4c8 and 5 in r4c7. Then, consider whether it’s possible that the arrow in r6c7/8 does not contain a 2. If it doesn’t, the next lowest available digits are 4 and 7.