Artisanal Sudoku, Volume 135

1. Scenic Route

• Normal sudoku rules apply (fill each row, column, and 3x3 box with the digits 1-9 once each), and all clues are standard.

• Correctly placed digits clear the fog around them.

• Along orange (entropic) lines, every set of three adjacent cells must contain one low digit (1-3), one middle digit (4-6), and one high digit (7-9).

• Digits in cells separated by a V sum to 5.

• Digits in cells separated by an X sum to 10.

• Digits in cells separated by a white dot are consecutive.

• Digits in cells separated by a black dot have a 1:2 ratio.

• Very rough difficulty estimate: 4/10

Play online: SudokuPad

New to variant sudoku? Check out these beginner-friendly guides to killer cages and other popular rulesets.

---

If you aren’t familiar with the most important two-digit number in variant sudoku, I’m honored to be the one to tell you that 1+2+3+4+5+6+7+8+9 = 45. In appreciation of this, I made Volume 45 of Artisanal Sudoku a special, non-paywalled edition, and I did it again with Volume 90.

And now, the third time around, the tradition continues. I hope you enjoy the bonus puzzles and the hints below, and if you’re not a premium subscriber already, I hope you’ll consider signing up. For just $5/month, you can get this much content every week, along with full access to the archive.

Some may argue, quite fairly, that this is too many puzzles. But even if you don’t have time to solve them all, I hope you’ll still consider signing up, because it takes time, effort, and money (in the form of payments to contributors) to put together a new slate of puzzles each week, and the more support I have from premium subscribers, the more time, effort, and money I’m able to put right back into making this newsletter the best it can possibly be.

Alright, that’s enough of that, let’s get back to the puzzles. Whatever tier you’re subscribed at, thank you so much!

---

2. Roadblocks

• Normal sudoku rules apply (fill each row, column, and 3x3 box with the digits 1-9 once each), and all clues are standard.

• German whispers: along green lines, digits must differ from their neighbors by at least 5.

• Digits in cells with a shaded square must be even.

• Digits in cells with a shaded circle must be odd.

• Digits in cells separated by a V sum to 5.

• Digits in cells separated by an X sum to 10.

• Very rough difficulty estimate: 5/10

Play online: SudokuPad | F-Puzzles

---

3. Silent Partner

Thanks so much to BremSter for recording a solve video of the puzzle below! Check that out here, and go ahead and subscribe to his channel while you’re at it—if you like the puzzles here, I’m confident you’ll like the puzzles BremSter features.

• Normal sudoku rules apply (fill each row, column, and 3x3 box with the digits 1-9 once each), and all clues are standard.

• Region sum lines: box borders divide each blue line into segments with the same sum.

• Killer cages: digits cannot repeat within a cage.

• Very rough difficulty estimates: 8/10, 6/10

Play online: SudokuPad | F-Puzzles

Extra clues: SudokuPad | F-Puzzles

---

Some other puzzles I enjoyed this week:

• Ele-en, by Qodec

• Peevers, by rockratzero

• Power-Sum Lines, by wuc

• RAT RUN 9: Shock Value, by Marty Sears (you’re probably familiar with these if you watch Cracking the Cryptic, but if not, let me assure you that the whole series is fantastic)

---

4. Timberwolf

• Normal sudoku rules apply (fill each row, column, and 3x3 box with the digits 1-9 once each), and all clues are standard.

• Killer cages: the sum of the digits inside each cage is equal to the small number in the top left corner.

• Thermometers: digits on thermometers increase from the bulb.

• Digits in cells separated by a V sum to 5.

• Very rough difficulty estimate: 6/10

Play online: SudokuPad | unshaded | F-Puzzles

---

5. True or False

• Normal sudoku rules apply (fill each row, column, and 3x3 box with the digits 1-9 once each).

• Digits cannot repeat on the indicated diagonals.

• The sum of the digits inside each cage is equal to the small number in the top left corner, except that each 3x3 box is either true or false. If a box is true, all of its cage sums are correct; if a box is false, all of its cage sums are incorrect.
  Two false boxes cannot be orthogonally adjacent (e.g. if box one is false, then boxes two and four must be true).

• The digit in the cell with a shaded circle must be odd.

• Very rough difficulty estimate: 9/10

Play online: SudokuPad | F-Puzzles

Two notes/clarifications:

• The rule about orthogonally adjacent boxes is a restriction on false boxes only. It is still permitted for two true boxes to be orthogonally adjacent.

• In case it’s difficult to see under the diagonal, the cage sums in r1c1, r2c2, and r4c4 are 8, 9, and 6, respectively.

---

Thanks for subscribing to Artisanal Sudoku! Feedback is always appreciated, just leave a comment, reach out on Twitter X, or reply to this email. If you liked these puzzles, you probably know someone else who’d like them too, so please spread the word. If you’re interested in submitting a puzzle, click here for more information. And if you want to try more of my puzzles—including several that are tougher than the ones you’ll find here—check out my page on Logic Masters Deutschland.

This week’s meta-description:
Feel free to double-check my math, but I’m pretty sure 135 is a multiple of 45, which means it’s time for another special edition, with bonus puzzles and hints for all!

---

Hints

Full disclosure: the hints don’t always include images. I try to throw some in when I feel like it might be especially helpful, but I could probably stand to do so more often. If you are (or are considering becoming) a paid subscriber and feel strongly about whether there should be more or fewer images in the hints, let me know about it!

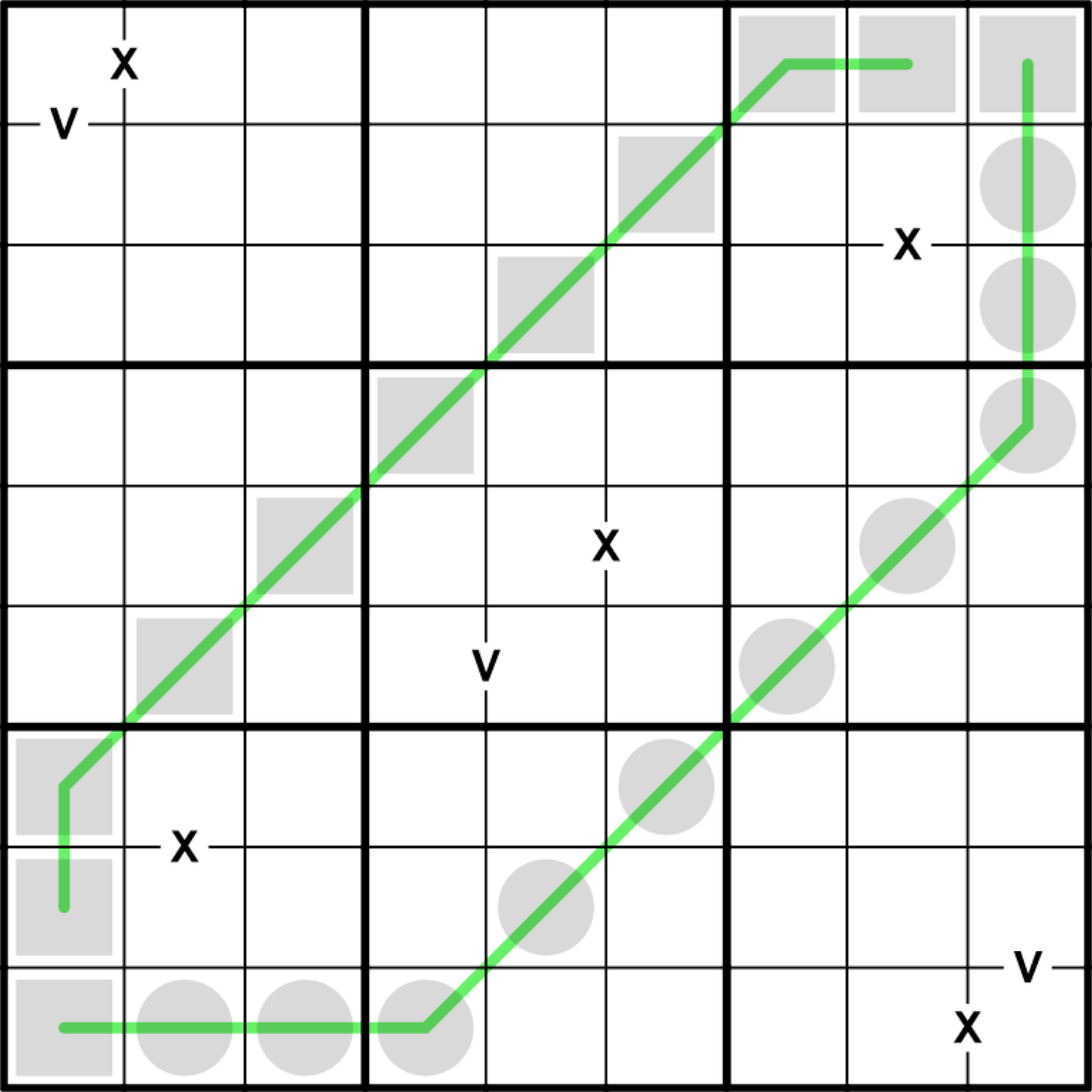
Scenic Route

1. If this is your first time encountering entropic lines, here’s a very important thing to know: the “every set of three adjacent cells” part of the rule means digits form a cycle that repeats over the entire length of the line. I can’t really give an example that’s specific to this puzzle because the fog obscures the line(s), so I’ll use the image below to illustrate it instead.

   

   The thermometer determines that the first three digits on the line are low, middle, and high, in that order. The fourth digit (r2c3) must differ in entropy from the second and third, so it must be low. The fifth digit (r2c2) must differ from the third and fourth, so it must be a middle digit, and so on. If at any point the cycle is broken, the entropic line would no longer be valid.

2. Here, the initially-visible entropic line occupies at least three cells: r9c1, r9c2, and r9c3, so the digits in those cells must each have a different entropy. The digits in r9c1 and r9c2 sum to 5, but 2 and 3 have the same entropy, so they must be 1+4.
   The digits in r9c2 and r9c3 sum to 10, so the options are 1+9 and 4+6, but 4 and 6 have the same entropy, so they must be 1+9, with 1 on the V in r9c2.

3. This puts 4 on the V in r9c1, which means the fourth digit on the line, in r8c3, must be another middle digit. It can’t be 4 by sudoku, and 5 can never appear on a black dot, so it must be 6.

4. Any time a white dot separates two digits on an entropic line, those digits must be 3-4 or 6-7.

5. If you get a little tripped up in box nine, consider where 7 can go in box eight, and then row eight.

Roadblocks

1. If 4 appears on a German whisper, it must be next to 9, and similarly, if 6 appears on a whisper, it must be next to 1. But every digit on the top-left whisper is even, so none of them can be 1 or 9; therefore, the only digits that can appear on the top-left whisper are 2 and 8.

2. The logic described in hint #1 puts a 28-pair in r7c1 and r8c1, which means the digit in r9c1 is 4 or 6. This is resolved by the V in box one, which must contain a 14-pair. Similar logic applies at the other end of the whispers in box three, where the X in box one is resolved by the fact that the digit in r1c9 is 4 or 6.

3. An important characteristic of German whispers is that digits alternate between low (from 1-4) and high (from 6-9) (this is sometimes referred to as low/high polarity). The bottom-right whisper occupies an even number of cells (12), which means the digits at each end will have the opposite polarity. Since the digit in r9c1 is high (as resolved by the V in box one), the digit in r1c9 is low, and therefore must be 4.

4. Consider what can go on the X’s in (appropriately enough) boxes three and seven. Both boxes contain a 28-pair on one whisper, and a 6-1 or 4-9 sequence on the other, leaving 3+7 as the only option for the X.

5. The bottom-right whisper is not quite as constrained as the other one, since the low digits can be 1 or 3 and the high digits can be 7 or 9—but there’s still pressure due to the fact that 3 and 7 can’t be adjacent on a whisper. This means, for example, the digit in r5c8 can’t be 3, because one of the digits in r4c9 or r6c7 has to be 7, and the digit in r8c5 can’t be 7 for the same reason.

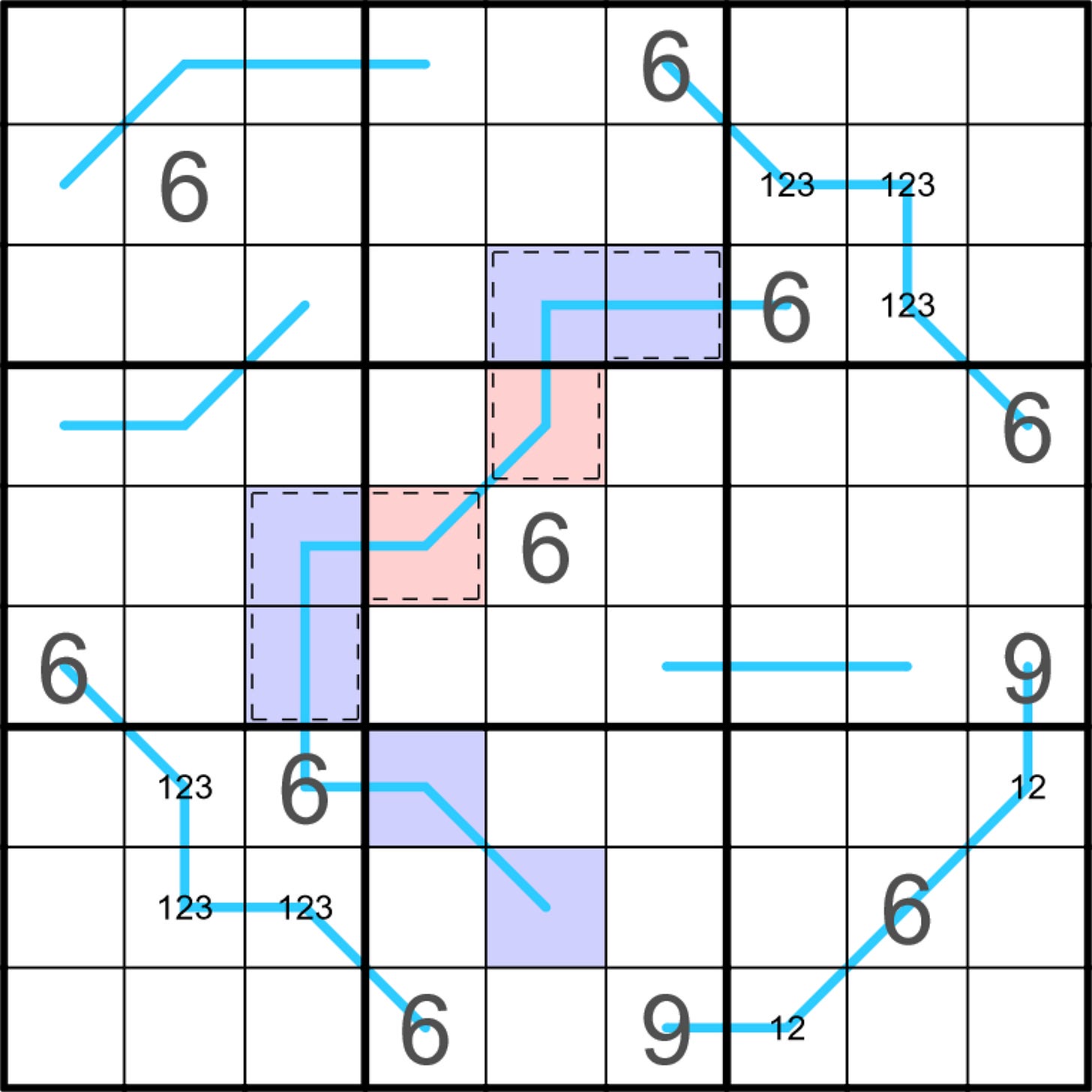
Silent Partner

1. The sum of the three digits on the region sum line segment in box three is equal to the digit in r1c6, and also to the digit in r4c9, which means the same digit is in those two cells (and must be 6 or greater). Then, consider where that digit can go in box three: it can’t be on the line (because the other two digits would need to sum to zero), and the only other cell not ruled out by sudoku is r3c7.
   The same logic can be used in the bottom-left corner to prove that r6c1, r7c3, and r9c4 contain the same digit, and in fact this digit must be the same as the region sum digit in the top-right, because r3c7 and r7c3 are one-cell segments on the same line.

2. This digit can now be placed in the remaining three boxes by sudoku, in r2c2, r5c5, and r8c8. The most significant of these is r8c8, because it’s part of a three-cell line segment that equals the digit in r6c9/r9c6. As noted above, the digit in r8c8 is at least 6, but now it can be no greater than 6, which means it must be 6, with a 12-pair in r7c9 and r9c7, and 9s in r6c9 and r9c6.

3. The region sum line that snakes through the middle of the grid now contains four two-cell segments that sum to 6; these segments can consist of 1+5 or 2+4, and this is where the cages come in. The pair of digits in r3c5/r3c6 can’t repeat in the cage, so the digit in r4c5 must be from the other pair (i.e. if 2+4 is on the line in box two, then the digit in r4c5 is 1 or 5, and vice versa).
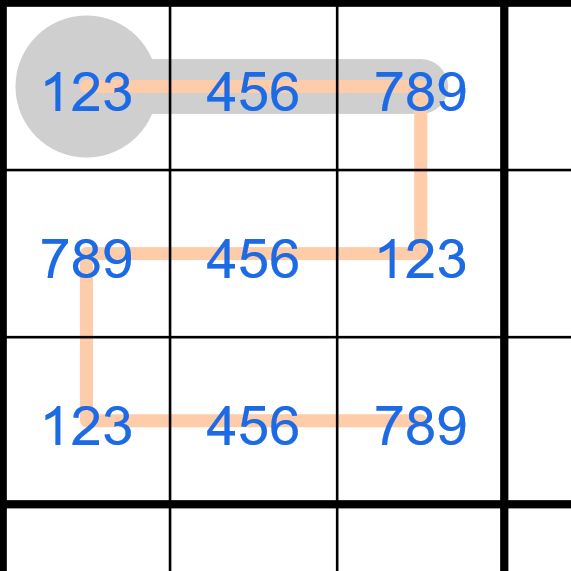
   The same logic applies with the other cage, so the line segment in box five contains a different pair than the line segments in boxes two and four, which must therefore contain the same pair. The pair on the segment in box eight must also be different from the pair in box five, because otherwise both digits would need to be stuffed into r2c6.

4. The result of all this might look something like this, where the blue cells contain one pair of digits that sum to 6, and the red cells contain the other.

   

   The important thing to note at this point is that each pair contains either 1 or 2, both of which are also on the region sum line segments in boxes three, seven, and nine. Among other things, this means:
   - the blue 1 or 2 is in r2c7 or r2c8 in box three, and in r7c2 or r8c2 in box seven, which means the only place for it in box one is r1c1
   - the blue 1 or 2 in row nine must be in r9c7, which means in column nine it must be in r5c9
   - once the digit in r9c7 is blue, the digit in r7c9 is red, and now the only place in row nine for the red 1 or 2 is r9c5
   - the red 1 or 2 in column six must now be in r2c6

5. Also, at the point shown in the image above, 9 can be placed in box five. Then, consider where 9 can go in boxes three and seven, and from there it can be placed in boxes one, two and four. Placing these 9s should make it possible to fully shade the 1s and 2s (which also makes it possible to place 3 in boxes three and seven).

6. Once you’ve determined that the digit in r1c1 is 1 or 2, consider whether it’s possible that the three-cell region sum line segment in box one doesn’t contain 3. If it doesn’t, it would sum to at least 10 (1+4+5). So there is a 3 on the line in box one, and by sudoku it must be in r1c3, and all the remaining 3s can be placed from there.

7. The digit in r1c4 must be at least 6, but 6 and 9 are ruled out by sudoku, and once 3 is placed in r1c3, 7 can be ruled out as well (because a set of three different digits that sum to 7 can never include 3).

Timberwolf

1. A three-cell 8-cage always contains 1, so the digit in r7c3 is at least 2. But the digit in r3c7 is at most 6, because the 24-cage contains 7+8+9, so the central thermometer is forced to contain a 2-6 sequence.

2. Placing 2 in r7c3 means the box seven cage must contain 1+3+4. The other 8-cage must now contain 1+2+5 (otherwise, there would be four cells in column two that contain digits from 1, 3, and 4), and the digit in r2c2 must be 5 because it needs to be possible to place a lower digit in r1c1.

3. The digits in r4c4 and r6c6 must be at least 3 (due to their positions on their thermometers), but 3, 4, and 5 are on the central thermometer in box five, so the minimum value for r4c4 and r6c6 is pushed up to 6.
   Among other things, this means the digit in r4c8 is at least 8, creating a 789-triple in column eight. The 20-cage can now only have one digit from 789 (in r8c7), which means the only combination that works is 5+6+9.

4. Consider where 8 and 9 can go in row one, and then where 7 can go in column two. Also, once you’ve made some more progress with 7s, look at where 8 can go in box five, and then box four.

True or False

1. There’s no low-hanging fruit in this one—even the incorrect cage sums are chosen to seem possible in isolation. But the problem is in box five: if it’s a true box, then by the Rule of 45 the digit in r6c6 would be 9, but now there’s nowhere in the box for 6. (There are a few other ways to see why box five must be false, all related to the fact that two two-cell 6-cages and two two-cell 12-cages can never coexist in a single box.)

2. So box five must be false, which means (because false boxes can’t be orthogonally adjacent) the even boxes must be true.
   Then, consider which digit can go in r5c5. The 16-cage contains 7+9, which means the 14-cage in box four contains 6+8, and the 4-cages contain 1+3, which means the 7-cage in box two contains 2+5, and now the only digit left that can appear in r5c5 is 4.

3. Once you’ve fully pencil-marked the “true” boxes adjacent to box five, you might wind up in a position like this:

   

   Note that each corner cell has a number of different digits looking at it. The digit in r1c9 can only be 5 or 6, and there is similar pressure on r1c1 (256), r9c1 (25), and r9c9 (57). And since these cells all see each other (by sudoku or by the diagonals), three of them contain a 256-triple, which means the digit in r9c9 must be 7.

4. There is more sudoku that can be done in box five—5 can be placed in r5c6, and there is a 123-triple in column four, which places the 7 in box four. Then, consider where 6 and 7 can go in box five: they form a pair in r4c5 and r4c6, but 7 can’t be in r4c6 because that would make the 12-cage correct. So 6 is in r4c6, which places 5 in r1c9. By sudoku, the only odd digit that can go on the circle in r2c9 is 9, so the 14-cage is correct and therefore box three is true.

5. The 6-cage in box three must contain 2+4, which means the 4 in column nine is in r7c9 or r8c9, and that means the 4 in row nine is in r9c2 or r9c3. A four-cell 11-cage can never contain 4, so box seven must be false.
   Box one is also false, which can be proven in a few different ways, including that the digits in r1c1, r1c9, and the 6-cage in box three make it impossible to correctly fill the 7-cage in box one.

6. Consider where 7 can go in box one (keeping in mind that it can’t repeat on the diagonal), and then where 2 can go (keeping in mind that the cage sums in box one must be incorrect).

7. Consider where 8 and 9 can go on the positive (i.e. upward-sloping) diagonal.