Artisanal Sudoku, Volume 180

1. Chelae

• Normal sudoku rules apply (fill each row, column, and 3x3 box with the digits 1-9 once each), and all clues are standard.

• Cages: the sum of the digits inside each cage is equal to the small number in the top left corner (if given), and digits cannot repeat within a cage.

• Very rough difficulty estimate: 3/10

Play online: SudokuPad | unshaded

New to variant sudoku? Check out these beginner-friendly guides to cages and other popular rulesets.

---

Incredibly, this volume marks four full sets of 45, which means—as it did for Volumes 45, 90, and 135—there’s no paywall in this one! Below the recommendations you’ll find two more bonus puzzles, and below them you’ll find a full set of hints.

If you like what you see (or, frankly, even if you don’t 😜), I hope you’ll consider becoming a paid subscriber, which at $5/month gets you bonus puzzles and hints every week, plus full access to the archive.

If that’s not something you can afford right now, that’s ok, you can still support Artisanal Sudoku by simply enjoying the puzzles (and if you get a chance to mention it to a friend, even better). Whatever form your support takes, thanks so much! I’m already excited about the next 45, and the 45 after that, and…

---

2. Ruche

• Normal sudoku rules apply (fill each row, column, and 3x3 box with the digits 1-9 once each), and all clues are standard.

• Renban lines: purple lines contain a non-repeating set of consecutive digits in any order.

• Quadruple circles: a digit inside a white circle must appear in one of the four cells surrounding that circle.

• Very rough difficulty estimate: 5/10

Play online: SudokuPad

---

3. Triumvirate

Check out this puzzle on BremSter’s YouTube channel!

• Normal sudoku rules apply (fill each row, column, and 3x3 box with the digits 1-9 once each), and all clues are standard.

• Digits cannot repeat on the indicated diagonal.

• Arrows: the sum of the digits along an arrow is equal to the digit in the connected circle, and these digits can repeat if allowed by other rules.

• Entropic lines: along orange lines, every set of three adjacent cells contains one low digit (1-3), one middle digit (4-6), and one high digit (7-9).

• Digits in cells separated by a black dot have a 1:2 ratio.

• Very rough difficulty estimates: 9/10, 6/10

Play online: SudokuPad

Extra clues: SudokuPad

---

Some other puzzles I enjoyed this week:

• I shall call him squishy, by PjoeterBliep

• Dutch Flat Mates: A-Sums, by Flinty

• Modulenburg, by RockyRoer

• Suburbia, by dumediat (this one’s from over a year ago, but it was new to me)

---

4. London Fog

• Normal sudoku rules apply within the 9x9 grid (fill each row, column, and 3x3 box with the digits 1-9 once each).

• Dynamic fog: correctly placed digits clear the fog around them, and some digits reveal clues outside the grid.

• Skyscraper clues: clues outside the grid indicate the number of digits visible in that direction (where higher digits block the view of lower digits). (Cells outside the grid without clues do not need to be filled.)

• Thermometers: digits on thermometers increase from the bulb.

• Digits in cells separated by an X sum to 10.

• Very rough difficulty estimate: 5/10

Play online: SudokuPad | version without fog

If you’re new to skyscraper clues, here are some examples of how they work, where the yellow digits are “seen” from the left and the purple digits are “seen” from the right:

For the 5-clue (looking from the left across the top row):

• 1 is seen (the digit immediately adjacent to the clue is always visible)

• 4 is seen because it’s greater than 1

• 7 is seen because it’s greater than 1 and 4

• 2 and 5 are not seen because they’re “hidden” behind 7

• 8 is seen because it’s greater than 7

• 3 and 6 are hidden behind 8

• 9 is always visible

…for a total of five visible skyscrapers.

---

5. Au Gratin

• Normal sudoku rules apply (fill each row, column, and 3x3 box with the digits 1-9 once each).

• Ten lines: gray lines can be divided into one or more segments, each of which contains digits that sum to 10. Digits may repeat on a line or within a segment if allowed by other rules.

• Quadruple circles: a digit inside a white circle must appear in one of the four cells surrounding that circle.

• Digits in cells separated by a (smaller) white dot are consecutive.

• Very rough difficulty estimate: 8/10

Play online: SudokuPad

---

Thanks for subscribing to Artisanal Sudoku! Feedback is always appreciated, just leave a comment, reach out on Bluesky, or reply to this email. If you liked these puzzles, you probably know someone else who’d like them too, so please spread the word. If you’re interested in submitting a puzzle, click here for more information. And if you want to try more of my puzzles—many of which are tougher than the ones you’ll find here—check out my page on Logic Masters Deutschland.

This week’s meta-description:
Celebrating four complete sets of 1-9 worth of sudokus.

---

Hints

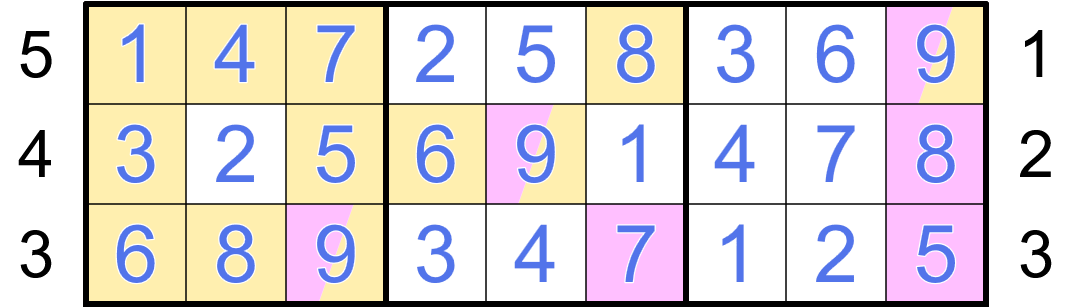
Chelae

1. Several of the cages have only one possible fill:
   4 = 1+3
   6 = 1+2+3
   16 = 7+9
   17 = 8+9
   24 = 7+8+9

2. The nine-cell cages contain every digit. The only place for 4 in the left nine-cell cage is r6c4, and then the only place for 3 is r5c4. Similarly, 6 and 7 can be placed in r4c6 and r5c6 in the right nine-cell cage.

3. Consider where 7 can go in box four: by sudoku, it has to be in r4c2, which places 7 in the 24-cage (r8c1) and then the 16-cage (r7c4).

4. The two-cell 6-cage in column one has to contain 2+4 (because the 1 in the column is in the 4-cage), and by sudoku the 4 is in r7c1. The digits in r7c3 and r8c3 have to appear somewhere in box four without repeating in their cage, so they must be the same as the digits in r4c1 and r6c1, which are 1 and 2. Then, consider where 1 and 2 can go in column two, and then where 4 can go.

5. Placing 4 in r3c2 puts 9 in r3c3, which resolves the 89-pair in the 17-cage. Then, consider where 9 can go in the right nine-cell cage.

6. Consider where 6 and 7 can go in box three, and then boxes one and two.

Ruche

1. The horizontal renban in row three is under a lot of pressure: the digit in r3c2 is at most 4, and the digit in r3c4 is at least 6, so those must be the correct digits, with 5 in r3c3. Similar logic can be used to fill the horizontal renban in row seven.

2. Placing 4 and 5 in row three puts a 45-pair on the quad circle in box three, and the digit in r2c9 can’t be 5 because both 4 and 6 would be unavailable to place on the renban in r1c8.
   Similar logic applies to 5 and 6 in box seven. In fact, this puzzle is fully rotationally symmetric (which is not something I like to do often, but with this one it all sort of fell into place), which means any logical step you find in one part of the grid can also be done in the opposite part (i.e. rotated 180 degrees) with low and high digits reversed. So I’m not going to keep pointing it out every time 😀

3. The 9 on the box three quad circle is in row three, which means the 9 on the box two/five quad circle is on the renban in box five. This does a few things:
   - the renban contains 789, so the digit in r5c3 is 7 or 8, and is the same as the digit in r3c5 (consider where that digit can go in row two)
   - there is only one place for 9 in column seven

4. The vertical renban in box three has to contain 678—all other options are ruled out by the quad circle or the two-cell renban—and since the digit in r5c3/r3c5 also appears in r2c7, the 6 in box three has to be in r1c7, which places 6 in box one (r2c3). Then, consider where 9 can go in column three.
   (And, again, this logic is all symmetrical.)

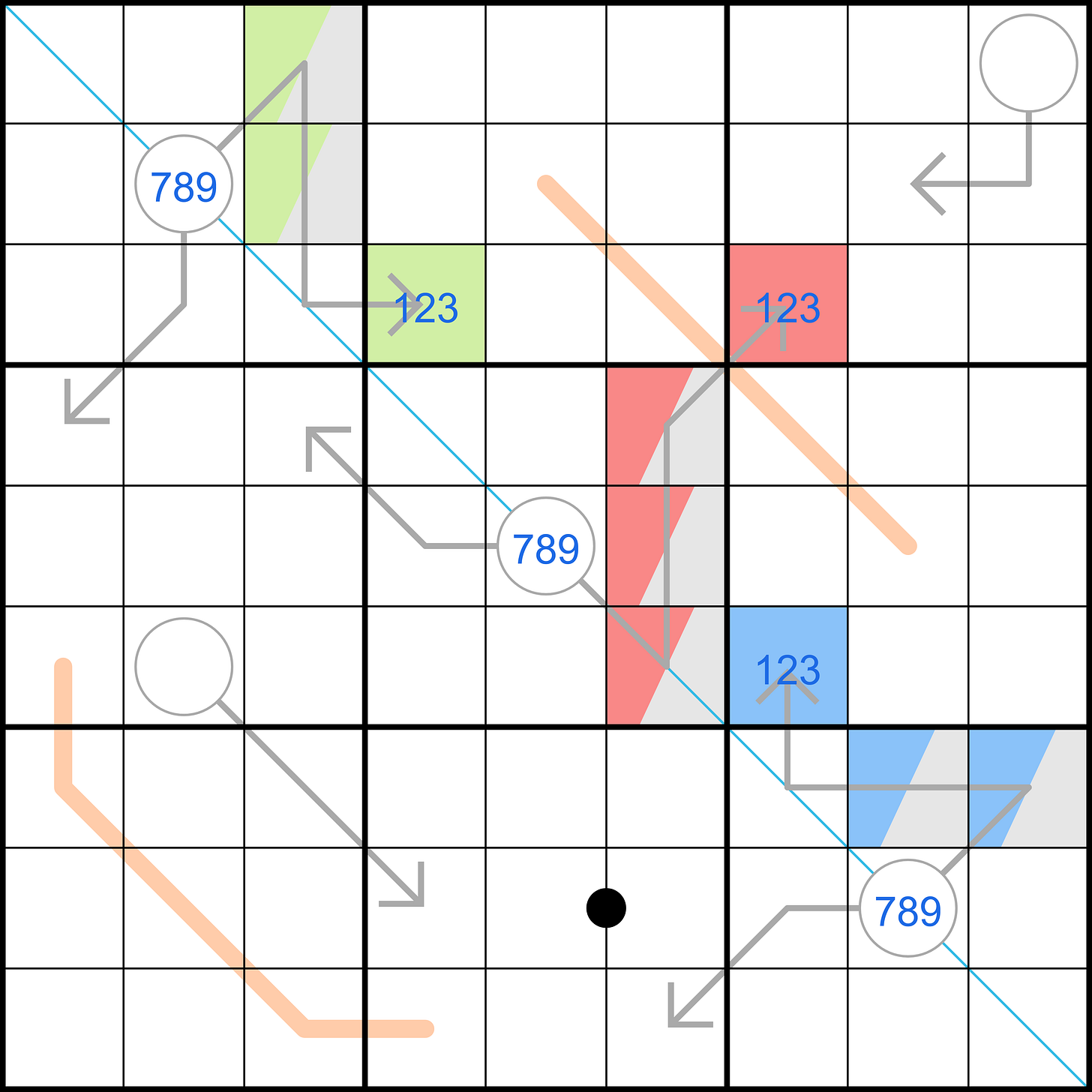
Triumvirate

1. If a four-cell arrow contains four different digits, it would sum to at least 10, so each of the four-cell arrows has a repeated digit, so the following things are forced by sudoku:
   - the digit in r3c4 repeats in r1c3 or r2c3
   - the digit in r3c7 repeats in r4c6, r5c6, or r6c6
   - the digit in r6c7 repeats in r7c8 or r7c9
   Also, the repeated digits can’t be greater than 3 (a repeated 4 would bring the sum to at least 11), and the arrow sums are all at least 7 (1+1+2+3 = 7). Since the circles are all on the diagonal, they contain a 789-triple.

   

   This shows the digits that repeat on the four-cell arrows, with the half-shaded cells representing possible positions within a box (i.e. the green digit is in r1c3 or r2c3 in box one).

2. Consider whether it’s possible for any two of the digits in r3c4, r3c7, and r6c7 to be the same. If so, it would have to be the digits in r3c4 and r6c7—green and blue in the image above—but both of those digits repeat on the four-cell arrows in boxes one and nine, so if they’re the same they would be ruled entirely off the diagonal (r4c4 and r6c6 would be seen by sudoku, and obviously that digit could not be in the circle in r5c5).

3. The takeaway from hint #2 is that the digits in r3c4, r3c7, and r6c7 form a 123-triple. And these are the digits that repeat on the four-cell arrows, so wherever 3 is, its arrow must now contain 1+2+3+3, to sum to 9. That accounts for 9 on the diagonal, so wherever 2 is, its arrow must contain 1+2+2+3, to sum to 8. And the final arrow contains 1+1+2+3 to sum to 7. So each four-cell arrow is made up entirely of digits from 123.

4. There are now a number of 123-triples that see the two-cell arrows connected to the circles on the diagonal. The arrows connected to the circles in r5c5 and r8c8, in fact, can’t contain a digit from 123 in either cell—so they must sum to 8 and 9, which can work if one contains 4+4 and the other contains 4+5.

5. Consider where 4 can go on the diagonal: there’s at least one 4 on the two-cell arrow connected to the circle in r5c5, and wherever it is it will see r4c4, and similar logic applies in box nine, so 4 has to be in r1c1.

6. There is now a 56-pair in r4c4 and r9c9, both of which see r9c4. The digit in r9c4 can’t be 4 either, because at least one of the digits in r5c4 and r9c6 is 4, and it also can’t be from 123, because that would put a low digit in r7c1 (because the nature of entropic lines is that the three sets form a cycle that repeats over the length of the line). So it must be from 789, which means the digit in r7c1 is also from 789, and the digits in r6c1 and r9c3 (which can’t be low because the latter sees the 123-triple in column three) are from 456.
   The digit in r9c3 can’t be 4 using similar logic—at least one of the digits in r4c3 and r9c6 is 4—which creates a 56-pair in row nine, placing 4 in r9c6. Then, consider what can go on the black dot, and then where 6 can go in box nine.

7. Consider where 1 can go in row six, and also where the low digit(s) can go on the box two/six entropic line.

8. It may take some progress with sudoku to resolve the order of the middle and high digits on the box two/six entropic line, but there should eventually be a point where all three digits from one of those sets see r3c6.

London Fog

1. Consider whether it’s possible for the X at the bottom of column eight to contain 4+6: it isn’t, because there are two digits between r8c8 and r9c8 on the thermometer. So one of the digits on the X is from 123 and the other is from 789 (nevermind for now that 1 and 9 can be ruled out by the thermometer).
   If the high digit is in r9c8, the skyscraper clue is impossible: in order for four digits to be seen, the digit immediately adjacent to the clue can’t be greater than 6. So the digit in r9c8 is low and the digit in r8c8 is high, but if that digit is 8 or 9 the skyscraper clue is broken again—the maximum number of visible digits would be three.
   What’s left after all this is that the digit in r8c8 has to be 7, which puts 3 in r9c8, and 4 and 6 in r9c9 and r8c9.

2. Following through on the logic described in hint #1 should make it possible to fill every cell in box nine and on the thermometer that crosses through it, revealing a 3-clue on the left side of row seven. But there are already three digits in row seven that will always be seen: the 9 in r7c9, the 8 in r7c8, and whatever digit is in r7c1. If that digit is anything other than 7, then the 7 in the row will also be seen, which would require a skyscraper clue of 4 or greater.

3. Once you’ve revealed the 2- and 4-clues at the top and bottom of column two, consider where 8 can go in the column. It can’t be in r8c2 because the clue looking upward would be exactly 3, and it can’t be in r2c2, r3c2, or r4c2 because the clue looking downward would be greater than 2—so it must be in r1c2.

4. Similar logic can be used once the 2-clue on the right side of row two is revealed: the 8 in the row is somewhere to the right of the 9, so both 8 and 9 will always be seen, and the digit in r2c9 will always be seen as well, so if that digit is not 8 there will be at least three digits visible.

5. If the 9 in box three is in r1c8, then the clue at the top of the column would be 1, so 9 must be in r3c8. Then, consider where 5 can go in the box, and keep in mind that to satisfy the 2-clue the digit in r1c8 must be greater than the digit in r2c8.

6. If the digit in r6c2 is 7, the skyscraper clue at the bottom of column two would need to be 5.

Au Gratin

1. To state the obvious: it’s impossible for a ten line to have a one-cell segment (i.e. a single digit with a value of 10). The lines that cross into box one clearly can’t contain one four-cell segment, because the digits on them in boxes two and four would sum to at least 13 on their own, so to avoid a one-cell segment, both lines must contain exactly two two-cell segments (i.e. r1c3 + r1c4 = 10, r2c3 + r2c4 = 10, etc.).
   The digits on the ten lines in box one, therefore, are the low counterparts to the high digits on the lines in boxes two and four, and since the low digits can’t repeat in box one, the corresponding high digits are a set of the digits 6789.

2. Since 6 is in both quad circles in the left two columns, the 6 in box one is in r3c3, and with 7 unavailable in boxes two and four, the other digit on both white dots must be 5. Then, consider where 7, 8, and 9 can go in row three and column three.

3. In column six, 7 and 9 have to be in the bottom three cells. The ten line that occupies two of those cells consists of a single segment (it can’t be divided without creating a one-cell segment), so it can never contain 9. That means 9 is in r9c6, and 7 is on the line, accompanied by a 12-pair.

4. The five-cell ten lines in boxes three and seven must contain at least two segments (it’s impossible for five digits to sum to 10 without repeated digits), but they can’t contain 3 or more (again, that would imply that at least one segment is a single cell). So they contain exactly two segments, which means their digits sum to 20. The digits in the 789-triple in each box sum to 24, so, using the Rule of 45, the digits in r1c7 and r7c1 have to be 1 (which fully resolves the ten line in boxes eight and nine).

5. Each five-cell line consists of a two-cell segment and a three-cell segment, and the two-cell segment must contain 4+6. In box seven, the quad circle determines that the 46-pair is in r9c1/r9c2. But wherever 4 is in box one, it’s part of a two-cell ten line segment, and the 46-pair in box seven means that segment can’t be on the ten line between boxes one and four. So it must be on the line between boxes one and two, which resolves the other five-cell line: the 46-pair can’t be in r1c9/r2c9 because it would rule 4 out of box one entirely.

6. Consider where 1 can go in box two, then box one, and then box four. Then, note that the seven-cell ten line that includes r1c7 now has four 1s, and its other three digits are no greater than 4. This gives it a theoretical maximum sum of 16, so it can never contain two segments, which means the entire line sums to 10.

7. The other seven-cell line has a digit from 789 at each end, which gives it a theoretical minimum sum of 21 (ignoring that 1 can be ruled out of several cells, which makes the minimum even higher). So it must have more than two segments, but can’t have four because at least one of them would contain a single cell.
   This means there are two two-cell segments and one three-cell segment. The three-cell segment can’t be at the bottom-left because 1 can’t be placed in r8c4 or r7c5, and it can’t be at the top-right because neither 1 nor 2 can be placed in r5c7. So the three-cell segment is in the middle of the line (r5c7, r6c6, r7c5), with a two-cell segment at each end.
   The white dot in row nine (and the fact that 7 and 9 are already accounted for in box eight) means the digit in r9c3 can’t be 8, so it’s 7, which puts 3 on the ten line in r8c4.

8. Once 5 is placed in r6c6, 5 can no longer appear on the ten line in r5c7 or r7c5, because it’s part of a three-cell segment and the third digit would have to be zero. This may be useful for placing 5 in both column seven and box eight.